Latent Dirichlet Allocation
January 15, 2023
Introduction

Latent Dirichlet Allocation (LDA) is one of the most popular topic modeling Topic modeling is a technique in natural language processing that aims to automatically identify the underlying themes or topics in a collection of text documents. methods out there, even though it has been published back in 2003 by David Blei, Andrew Ng, and Michael Jordan.
LDA produces two output
- a probability distribution on words to represent topics
- a probability distribution on topics to summarize documents
So imagine you have the following set of sentences (a sentence is just a very short document):
- I like going running because it makes me feel good
- Let’s go swimming tomorrow morning!
- I’m going to play at a concert tonight
- The other day I saw a great pianist in the city streets
- I love working out while listening to rock music
LDA will find the following summarization for such sentences:
| Sentence | Topic A | Topic B |
|---|---|---|
| I like going running because it makes me feel good | 100% | 0% |
| Let’s go swimming tomorrow morning! | 100% | 0% |
| I’m going to play at a concert tonight | 20% | 80% |
| The other day I saw a great pianist in the city streets | 0% | 100% |
| I love working out while listening to rock music | 50% | 50% |
An the following representation for the two topics:
| Topic | running | swimming | play | concert | pianist | work out | rock | music |
|---|---|---|---|---|---|---|---|---|
| Topic A | 30% | 30% | 10% | 30% | ||||
| Topic B | 12% | 22% | 22% | 22% | 22% |
Ok, so how do we obtain such output?
Before diving into the algorithm let’s revise a couple of prerequisities.
Prerequisites
Poisson Distribution

Call center calls are a typical example of Poisson distribution
The Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event.
Example:
A call center receives an average of 180 calls per hour, 24 hours a day. The calls are independent: receiving one does not change the probability of when the next one will arrive. The number of calls received during any minute can be modeled as a Poisson probability distribution with mean 3:
with high probability the call center will receive 2 or 3 calls in a specific minute, but there is a small chance it will receive 0 or even 6.
This distribution makes this assumptions:
- The occurrence of one event does not affect the probability that a second event will occur \(\to\) events occur independently.
- Two events cannot occur at exactly the same instant; instead, at each very small sub-interval, either exactly one event occurs, or no event occurs.
If these conditions are true, then \(k\) is a Poisson random variable, and the distribution of \(k\) is a Poisson distribution.
Dirichlet Distribution
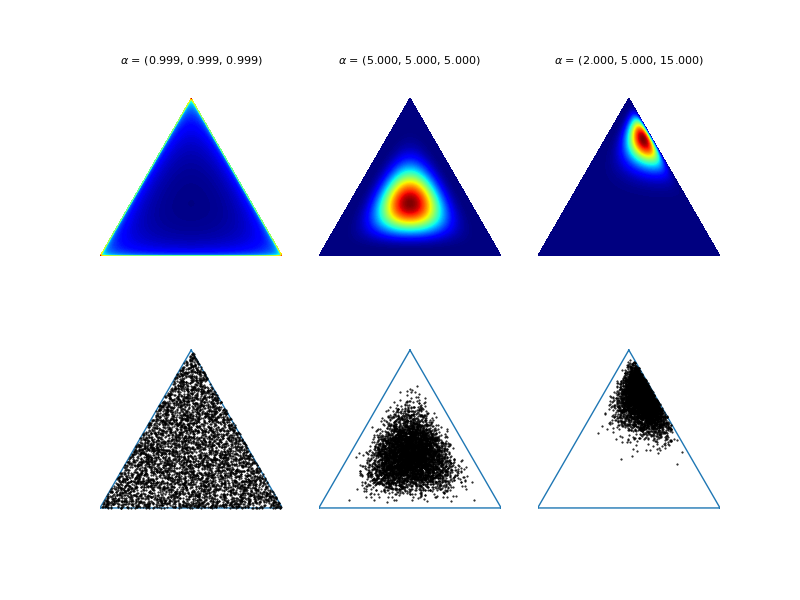
Some possible configurations for a Dirichlet distribution with 3 parameters. On top are shown the heat maps of the distribution, on the bottom are shown data points sampled from each configuration. Each vertex corresponds to an “entity”. In LDA entities are topics. Image credits to tboggs.
The Dirichlet distribution is a family of continuous multivariate probability distributions parametrized by a vector \(\alpha\) of positive reals.
I will explain it in a simple way, that I think makes it easy to grasp the rationale behind it.
Do you remember the Beta distribution? It is a continuous distribution that is usually dubbed as “the probability distribution of probabilities”, because it can only take values between \(0\) and \(1\).
The Beta distribution has two parameters: \(\alpha\) and \(\beta\).
- \(\alpha\)
an integer, the higher it is, the higher the probability of success is - \(\beta\)
an integer, the higher it is, the higher the probability of failure is
The Dirichlet distribution is a generalization of the Beta distribution. It is a probability distribution describing probabilities of outcomes. Instead of describing probability of one of two outcomes of a Bernoulli trial, like the Beta distribution does, it describes probability of \(K\) outcomes.
The Beta distribution is the special case of the Dirichlet distribution with \(K=2\).
The parameters are \(\alpha_1, \alpha_2, \dots, \alpha_K\) all strictly positive, defined analogously to \(\alpha\) and \(\beta\) of the Beta distribution.
Latent Dirichlet Allocation in depth
Assumptions

My attempt at generating a bag of words with DALLE
- “bag-of-words” assumption: the order of the words in a document doesn’t matter
- documents are exchangeable: the specific ordering of the documents in a corpus can also be neglected
A classic representation theorem due to de Finetti (1990) establishes that any collection of exchangeable random variables has a representation as a mixture distribution (a mixture of two or more probability distributions).
Notation and terminology
-
A word is the basic unit of discrete data, defined to be an item from a vocabulary indexed by \(\{1, \dots ,V\}\).
We represent words using unit-basis vectors that have a single component equal to one and all other components equal to zero.
Thus, using superscripts to denote components, the \(v\)-th word in the vocabulary is represented by a vector \(w\) such that \(w^v=1\) and \(w^u=0\) for \(u\neq v\). - A document is a sequence of \(N\) words denoted by \(\mathbf{w}= (w_1,w_2, \dots,w_n)\), where \(w_n\) is the \(n\)-th word in the sequence.
- A corpus is a collection of \(M\) documents denoted by \(C = \{\mathbf{w_1}, \mathbf{w_2}, \dots, \mathbf{w_M}\}\).
Algorithm
Assumption on documents generation
LDA assumes that documents are represented as random mixtures over latent topics, where each topic is characterized by a distribution over words.
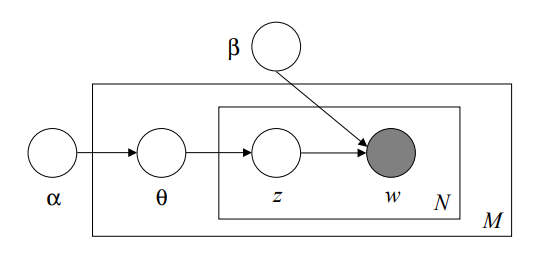
Graphical model representation of LDA. The boxes are “plates” representing replicates. The outer plate represents documents, while the inner plate represents the repeated choice of topics and words within a document.
LDA assumes the following generative process for each document \(\textbf{w}\) in a corpus \(D\):
- Choose \(N \sim Poisson(\xi)\)
- Choose \(\theta \sim Dir(\alpha)\)
- For each of the \(N\) words \(w_n\)
- Choose a topic \({z_n \sim Multinomial(\theta)}\)
- Choose a word \(w_n\) from \(p(w_n|z_n,\beta)\):
a multinomial probability conditioned on the topics \(z_n\).
where:
-
\(N \sim Poisson(\xi)\) means that we are sampling a number of words given the average number of words \(\xi\).
-
\(\theta \sim Dir(\alpha)\) means that we are sampling topic probabilities given the vector of Dirichlet parameters \(\alpha\).
if the number of topics is \(3\), \(\theta\) might look like \(\theta = (0.3, 0.5, 0.2)\). -
\({z_n \sim Multinomial(\theta)}\) means that we are sampling one out of the \(N\) topics, using \(\theta\) as our probability distribution over topics.
If we consider \(\theta = (0.3, 0.5, 0.2)\) we’ll have- \(z_n=z^1\) with \(30\%\) probability
- \(z_n\) = \(z^2\) with \(50\%\) probability
- \(z_n = z^3\) with \(20\%\) probability
where \(z^1, z^2, z^3\) are simply three variables that represent the \(3\) topics.
-
\(\beta\) is a matrix of dimensionality \(k \times V\) (number of topics times number of words in the vocabulary)
where \({\beta_{ij}=p(w^j=1|z^i=1)}\).
Assuming the generative model for a collection of documents, LDA then tries to backtrack from the documents to find a set of topics that are likely to have generated the collection.
Collapsed Gibbs Sampling
So now suppose you have a set of documents. You’ve chosen some fixed number of \(K\) topics to discover, and want to use LDA to learn the topic representation of each document and the words associated to each topic.
How do you do this? one way, known as collapsed Gibbs sampling, is the following:
1. Go through each document and randomly assign each word in the document to one of the K topics
2. for each document
1. for each word w in the document
2. reassign a new topic to w using the probability P
where \(P = P(z_i=j|z_{-i},w_i,d_i) \propto \frac{C^{WT}_{w_ij}+ \eta}{\sum^{W}_{w=1}C^{WT}_{wj}+W\eta}\times \frac{C^{DT}_{d_ij}+\alpha}{\sum_{t=1}^TC^{DT}_{d_it}+T\alpha}\)
left member of the expression:
- \(P(z_i=j)\) - the probability that token \(i\) is assigned to topic \(j\)
- \(z_{-i}\) - represents topic assignments of all other tokens
- \(w_i\) - Word (index) of the \(i\)-th token
- \(d_i\) - Document containing the \(i\)-th token.
right member of the expression:
- \(C^{WT}\) - the word-topic matrix
- \(\sum_{w=1}^{W}C_{wj}^{WT}\) - total number of tokens (words) in each topic
- \(C^{DT}\) - the document-topic matrix
- \(\sum_{t=1}^{T}C_{d_it}^DT\) - total number of tokens (words) in document \(i\)
- \(\eta\) - parameter that sets the topic distribution for the words. The higher the more spread out the words will be across he specified number of topics (\(K\))
- \(\alpha\) - parameter that sets the topic distribution for the documents. The higher the more spread out the documents will be across the specified number of topics (\(K\))
- \(W\) - the total number of words in the set of documents
- \(T\) - number of topics, equivalent of the \(K\) we defined earlier
We can iterate over the algorithm defined above until we find a stable representation of the matrices \(C^{WT}\) and \(C^{DT}\).
Conclusions

The end scene of the Jungle book by Zoltan Korda UK, 1942
In summary, Latent Dirichlet Allocation is a powerful tool for uncovering the underlying topics in a collection of text documents. We have seen how LDA works by analyzing the probability distribution of words in a text corpus and grouping them into different topics.
LDA has a wide range of applications in various fields such as natural language processing, information retrieval, and text mining. In natural language processing, LDA can be used to classify text into different categories or to understand the underlying themes in a set of documents. In information retrieval, LDA can be used to improve search results by understanding the topics of documents and in text mining can be used to extract insights from unstructured data.
Even though LDA is a very popular algorithm in the topic modeling realm, I suggest you to try out other more recent models, such as Top2Vec and BERTopic: The first one relies on applying the clustering algorithm HDBSCAN on high dimensional token embeddings (relying though on UMAP for dimensionaliy reduction), while BERTopic leverages transformers and a class-based TF-IDF procedure.
Se you soon!
Sources: